dome vs. sphenoid
All,
This should be a quick one, as I must be missing something obvious. The usual definitions of the "dome" and "sphenoid" crystal forms say something like this...
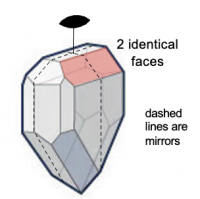
A dome has two crystal faces that can be related to each other by a mirror plane
*
A sphenoid has two crystal faces that can be related to each by a two-fold rotational axis.
Although my search was not comprehensive, none of the definitions I have seen deal with the case where the two faces can be related to each other by BOTH a mirror and a two-fold axis (as in the attached graphic). In that case, what form is it: a dome or a sphenoid?
There are other rules of preferring one symmetry element over another one in the accounting if both are present in the same crystal, e.g.,
* if a single axis produces more than one type of rotational symmetry (like a 2-fold and a 4-fold; i.e., different n’s), only count the higher n-fold rotation
*
if an axis produces both rotational and rotoinversional symmetry…
* if the n’s are the same, only count the rotational axis
*
if the n’s are different, only count the higher n-fold operation
...but in this case, I can't figure out how to compare the different symmetry operations (m vs. 2-fold), so these rules don't seem to apply.
Kent Ratajeski
Dr. Kent Ratajeski
Lecturer and Dice Mineralogical Museum Director
North Hall 081
Department of Geology, Geography, and Environment
Calvin University
3201 Burton St. SE
Grand Rapids, MI 49546
(616) 526-6769
https://calvin.edu/directory/people/kent-ratajeski
https://calvin.edu/dice
Hi Kent,
This is actually a pretty interesting question. As best I can tell, this question would ONLY be relevant for point group 2mm, because any point group of less symmetry would have only one symmetry element generating the form, and any point group of more symmetry would produce a form with more than two faces.
You’re correct that you can’t rely on the rules that you give in your message, because in the case of a 2-fold axis and an intersecting mirror plane, the “2-fold rotoinversion axis” (equivalent to the mirror plane) is actually situated perpendicular to the 2-fold axis. So rules that prioritize various symmetries along the SAME axis would not be relevant here. Since there are two different symmetry elements (oriented differently) that happen to produce the same form, my own personal answer would be that you could rightfully call it either a dome or a sphenoid. In the Perkins et al. textbook, their chart of forms lists point group 2mm has having a dome but NOT a sphenoid, but the reason for not check marking the sphenoid is not clear to me: https://geo.libretexts.org/Bookshelves/Geology/Mineralogy_%28Perkins_et_al.%29/10%3A_Crystal_Morphology_and_Symmetry/10.05%3A_Point_Groups_and_Crystal_Systems/10.5.01%3A_Forms_and_Point_Groups
Best,
Dan
DANIEL HUMMER
Associate Professor of Geology
SCHOOL OF EARTH SYSTEMS AND SUSTAINABILITY
MAIL CODE 4324
SOUTHERN ILLINOIS UNIVERSITY
PARKINSON LABORATORY 207
CARBONDALE, ILLINOIS 62901
daniel.hummer@siu.edumailto:daniel.hummer@siu.edu
P: 618.453.7386
SIU.EDU
[https://oit.siu.edu/enterprisesystems/email-sig-gen/images/Email-Logo-2023-maroon.png]
From: Kent Ratajeski via MSA-talk msa-talk@minlists.org
Sent: Monday, February 2, 2026 1:23 PM
To: msa-talk@minlists.org
Subject: [MSA-talk] dome vs. sphenoid
[EXTERNAL EMAIL ALERT]: Verify sender before opening links or attachments.
All,
This should be a quick one, as I must be missing something obvious. The usual definitions of the "dome" and "sphenoid" crystal forms say something like this...
-
A dome has two crystal faces that can be related to each other by a mirror plane
-
A sphenoid has two crystal faces that can be related to each by a two-fold rotational axis.
Although my search was not comprehensive, none of the definitions I have seen deal with the case where the two faces can be related to each other by BOTH a mirror and a two-fold axis (as in the attached graphic). In that case, what form is it: a dome or a sphenoid?
There are other rules of preferring one symmetry element over another one in the accounting if both are present in the same crystal, e.g.,
* if a single axis produces more than one type of rotational symmetry (like a 2-fold and a 4-fold; i.e., different n’s), only count the higher n-fold rotation
* if an axis produces both rotational and rotoinversional symmetry…
* if the n’s are the same, only count the rotational axis
* if the n’s are different, only count the higher n-fold operation
...but in this case, I can't figure out how to compare the different symmetry operations (m vs. 2-fold), so these rules don't seem to apply.
Kent Ratajeski
Dr. Kent Ratajeski
Lecturer and Dice Mineralogical Museum Director
North Hall 081
Department of Geology, Geography, and Environment
Calvin University
3201 Burton St. SE
Grand Rapids, MI 49546
(616) 526-6769
https://calvin.edu/directory/people/kent-ratajeski
https://calvin.edu/dice
Hi Kent!
I could be terribly wrong. So feel free to correct me if I am, but isn’t a mirror plane also symmetrically equivalent to a 2-fold rotoinversion? If so, wouldn’t this be comparing two axes of similar n (2-fold axis of rotation vs. 2-fold rotoinversion). Based on the rules you outlined, I would assume that you would only count the rotational axis. Thus, wouldn’t this be a sphenoid based on the definition you provided?
I don’t claim to be a crystallographer! So, I welcome input from those that are!
Ken
Sent from my iPhone
On Feb 4, 2026, at 4:04 PM, Kent Ratajeski via MSA-talk msa-talk@minlists.org wrote:
This message was sent from a non-IU address. Please exercise caution when clicking links or opening attachments from external sources.
All,
This should be a quick one, as I must be missing something obvious. The usual definitions of the "dome" and "sphenoid" crystal forms say something like this...
A dome has two crystal faces that can be related to each other by a mirror plane
*
A sphenoid has two crystal faces that can be related to each by a two-fold rotational axis.
Although my search was not comprehensive, none of the definitions I have seen deal with the case where the two faces can be related to each other by BOTH a mirror and a two-fold axis (as in the attached graphic). In that case, what form is it: a dome or a sphenoid?
There are other rules of preferring one symmetry element over another one in the accounting if both are present in the same crystal, e.g.,
* if a single axis produces more than one type of rotational symmetry (like a 2-fold and a 4-fold; i.e., different n’s), only count the higher n-fold rotation
*
if an axis produces both rotational and rotoinversional symmetry…
* if the n’s are the same, only count the rotational axis
*
if the n’s are different, only count the higher n-fold operation
...but in this case, I can't figure out how to compare the different symmetry operations (m vs. 2-fold), so these rules don't seem to apply.
Kent Ratajeski
Dr. Kent Ratajeski
Lecturer and Dice Mineralogical Museum Director
North Hall 081
Department of Geology, Geography, and Environment
Calvin University
3201 Burton St. SE
Grand Rapids, MI 49546
(616) 526-6769
https://calvin.edu/directory/people/kent-ratajeski
https://calvin.edu/dice
<Screenshot 2026-02-02 at 1.21.43 PM.png>
MSA-talk mailing list -- msa-talk@minlists.org
To unsubscribe send an email to msa-talk-leave@minlists.org